SINGLE-PIXEL IMAGING
Overview

FIG: Principle of single-pixel imaging.
Single-pixel imaging is a paradigm that allows images to be provided by a device that is only equipped with a single point detector. A single-pixel camera is an experimental set-up that measures the inner products of a scene under view with several user-defined patterns. A common implementation relies on the use of a digital micromirror device (DMD, see Figure above). Let $\boldsymbol{f} \in \mathbb{R}^{N}$ be the image of the object and $m_i$ be the measurement obtained loading the pattern $\boldsymbol{a}_i \in \mathbb{R}^{N}$ on the digital micromirror device. We have:
$m_i= \boldsymbol{a}_i^\top \boldsymbol{f} \quad$
The image $\boldsymbol{f}$ needs to be reconstructed from the full measurement vector $\boldsymbol{m} \in \mathbb{R}^{M}$, given the system matrix $\boldsymbol{A}$ that contains all the light patterns. The current trend consists in designing artificial neural networks to solve the reconstruction task, for which the SPyRiT package may prove useful.
Freeform Hadamard imaging
N. Ducros et al., 'Freeform Hadamard imaging: Back to the roots of computational optics', working document, 2025.
SPyRiT 3.0
J. Abascal et al., 'SPyRiT 3.0: an open source package for single-pixel imaging based on deep learning', Optics Express, 33(13), pp. 27988-28005, 2025.
This paper describes SPyRiT 3.0, an open source PyTorch-based toolbox capable of handling various simulation configurations and reconstruction methods based on deep learning. The modularity of SPyRiT enables the evaluation of various configurations and the rigorous benchmarking of reconstructions based on deep learning. Here, we compare several supervised and plug-and-play methods, including post-processing and iterative strategies.
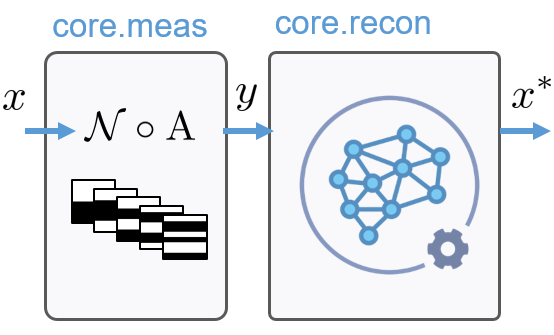
FIG: Typical SPyRiT pipeline involving input of an image x, simulation of the raw measurements y, and estimate of image x*.
The OpenSpyrit ecosystem

FIG: Overview of the OpenSpyrit ecosystem.
J.F.P.J. Abascal et al., 'Reproducible hyperspectral single-pixel imaging using the OpenSpyrit ecosystem', SPIE Photonics Europe, Unconventional Optical Imaging IV, 2024.
In this talk, we focus on the unrolled algorithms and the plug-and-play methods available in SPyRiT.
G. Benedeti Martin et al., 'OpenSpyrit: an ecosystem for open single-pixel hyperspectral imaging', Optics Express, 31 (10), pp.15599, 2023.
In this paper, we introduce OpenSpyrit, an open access and open source ecosystem for reproducible research in hyperspectral single-pixel imaging, composed of SPAS (a Python single-pixel acquisition software), SPYRIT (a Python single-pixel reconstruction toolkit) and SPIHIM (a single-pixel hyperspectral image collection). The proposed OpenSpyrit ecosystem responds to the need for reproducibility and benchmarking in single-pixel imaging by providing open data and open software.
Deep learning for image reconstruction
L. Mahieu-Williame et al., 'A fast computational approach for high spectral resolution imaging', SPIE Photonics Europe, 2022.
In this talk, we present reconstruction results from simulated and experimental hyperspectral data. We show that the EM-Net method generalizes very well to noise levels that are unseen during the training, despite having fewer learned parameters than alternative methods.


FIG: Hypercube acquired with the STL-10 cat (left) and Siemens star target (right) superimposed to a linear variable filter
A. Lorente Mur et al., 'Single-pixel image reconstruction from experimental data using neural networks', Optics Express, 29 (11), pp. 17097, 2021.
In this paper, we introduce the denoised completion network (DC-Net) method for the reconstruction from measurements that are corrupted by mixed Poisson-Gaussian noise. We propose to map the raw data from the measurement domain to the image domain based on a Tikhonov regularization. This step can be implemented as the first layer of a deep neural network, followed by any architecture of layers that acts in the image domain


FIG: Reconstruction using several methods. Left: ground-truth image acquired at low noise. Right: high noise image reconstructed using least squares, total variation regularization, Tikhonov regularization, Tikhonov regularization + BM3D, and DC-Net.
A. Lorente Mur et al., 'A recurrent neural network for compressive video reconstruction', IEEE ISBI, 2020.
We propose a deep-learning reconstructor that exploits the spatio-temporal redondancy in a video. In particular, we consider convolutional gated recurrent units that have low memory requirements. Our simulation shows than the proposed recurrent network improves the reconstruction quality compared to static approaches that reconstruct the video frames independently.
N. Ducros et al., 'A completion network for reconstruction from compressed acquisition', IEEE ISBI, 2020.
We proposed to interpret the reconstruction problem of single-pixel imaging as a Bayesian completion problem. Our idea is to estimate the missing measurements from those acquired. From this point of view, a network emerges that includes a fully connected layer that provides the best linear completion scheme. This network has a lot fewer parameters to learn than direct networks, and it trains more rapidly than image-domain networks that correct pseudo inverse solutions.
Pattern generalization
F. Rousset et al., 'A semi nonnegative matrix factorization technique for pattern generalization in single-pixel imaging', IEEE Trans. Comput. Imaging, 4(2), 284-294, 2018.
Real acquisitions require the spatial light modulator patterns to be positive while desired patterns typically have negative values. We have proposed to seek positive patterns that are linear combinations of the desired patterns with negative values. We refer to the problem of finding the positive patterns and the linear combinations as pattern generalization.

FIG: Overview of the pattern generalization approach
Adaptive imaging
F. Rousset et al., 'Time-resolved multispectral imaging based on an adaptive single-pixel camera', Opt. Express, 26(8), 10550-10558, 2018.
We have demonstrated experimentally a time-resolved multispectral acquisition scheme based on single-pixel imaging. Here, we used an adaptive strategy that allows acquisition and image reconstruction times to be reduced drastically with respect to conventional single-pixel approaches that are based on compressed sensing or full basis scans.

FIG: Fluorescence lifetimes recovered from time stack acquired in a phantom containing three fluorophores
F. Rousset et al., 'Adaptive basis scan by wavelet prediction for single-pixel imaging', IEEE Trans. Comput. Imaging, 3(1), 36-46, 2017.
We have proposed to choose patterns among a wavelet basis in an adaptive fashion and adopt a multiresolution strategy that exploits the set of measurements acquired at coarse scales to predict the set of measurements to be performed at a finer scales.

FIG: Adaptive acquisition in a Daubechies wavelet basis at increasing resolutions (compression ratios: 256:1, 68:1, 18:1, 5:1, 2:1)